Page 89 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

89

 (t ,t ) = R (t ,t ) /  (t ) (t ),
х 1
y 2
ху 1 2
1 2
ху
де  (t ),  (t ) – середні квадратичні відхилення процесів Х (t) і Y (t).
1
1
х 1
y 2
Інколи застосовують спрощену форму запису цього виразу:
 = R /  .
ху
х
ху
y
У випадку дискретного фіксування ординат випадкових процесів оцінка но-
рмованої взаємної кореляційної функції розраховується за формулою:
1 N m 
ρ xy   Xi  Yi m ,
(N  m - 1)  σ x  σ y i 1
де m = 0, 1, 2, 3… – число, яке визначає зсув по осі абсцис;
Х , Y i+m – нормовані ординати реалізації процесу Х в момент часу і і

і
процесу Y в момент часу i + m відповідно;
Взаємна кореляційна функція може відображатися у 4-х квадрантах. Якщо її
максимум знаходиться у першому чи другому квадрантах, то між статистично
випадковими процесами Х і Y існує позитивний кореляційний зв’язок (рис. 5.10).
Тобто, збільшення значин (ординат) одного із них обумовлює відповідне збіль-
шення значин другого.

 ху 1 2 t 2 1

0,8 t 1

0,6

0,4

0,2

0 с
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-0,2

-0,4

-0,6

-0,8

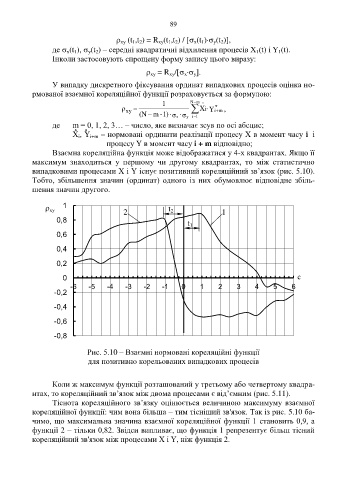
Рис. 5.10 – Взаємні нормовані кореляційні функції
для позитивно корельованих випадкових процесів

Коли ж максимум функції розташований у третьому або четвертому квадра-
нтах, то кореляційний зв’язок між двома процесами є від’ємним (рис. 5.11).
Тіснота кореляційного зв’язку оцінюється величиною максимуму взаємної
кореляційної функції: чим вона більша – тим тісніший зв'язок. Так із рис. 5.10 ба-
чимо, що максимальна значина взаємної кореляційної функції 1 становить 0,9, а
функції 2 – тільки 0,82. Звідси випливає, що функція 1 репрезентує більш тісний
кореляційний зв'язок між процесами Х і Y, ніж функція 2.