Page 87 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

87

З кореляційною функцією ця характеристика зв’язана загальновідомим
косинусперетворенням Фур’є. Позначається ця характеристика як S(), а її розмі-
2
2
2
рністю є добуток дисперсії процесу на час (м с, см с, Н с тощо).
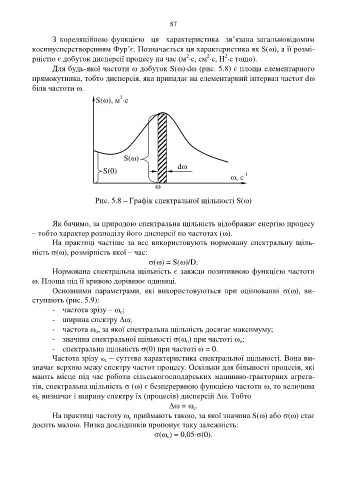
Для будь-якої частоти  добуток S()d (рис. 5.8) є площа елементарного
прямокутника, тобто дисперсія, яка припадає на елементарний інтервал частот d
біля частоти .

2
S(), м с

S()
d
S(0)
, с -1


Рис. 5.8 – Графік спектральної щільності S()

Як бачимо, за природою спектральна щільність відображає енергію процесу
– тобто характер розподілу його дисперсії по частотах ().
На практиці частіше за все використовують нормовану спектральну щіль-
ність (), розмірність якої – час:
() = S()/D.
Нормована спектральна щільність є завжди позитивною функцією частоти

. Площа під її кривою дорівнює одиниці.
Основними параметрами, які використовуються при оцінюванні (), ви-
ступають (рис. 5.9):
- частота зрізу –  ;
с
- ширина спектру ;
- частота  , за якої спектральна щільність досягає максимуму;
о
- значина спектральної щільності ( ) при частоті  ;
о
о
- спектральна щільність (0) при частоті  = 0.
Частота зрізу  – суттєва характеристика спектральної щільності. Вона ви-
с
значає верхню межу спектру частот процесу. Оскільки для більшості процесів, які
мають місце під час роботи сільськогосподарських машинно-тракторних агрега-
тів, спектральна щільність  () є безперервною функцією частоти , то величина
 визначає і ширину спектру їх (процесів) дисперсій . Тобто
с
 =  .
с
На практиці частоту  приймають такою, за якої значина S() або () стає
с
досить малою. Низка дослідників пропонує таку залежність:
( ) = 0,05(0).
с