Page 84 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

84

Звідси цілком зрозуміло, що у початковий момент часу (m = 0) нормована
кореляційна функція дорівнює одиниці. Усі інші її значини є меншими за 1.
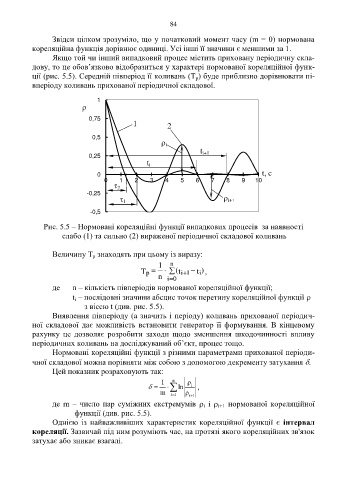
Якщо той чи інший випадковий процес містить приховану періодичну скла-
дову, то це обов’язково відобразиться у характері нормованої кореляційної функ-
ції (рис. 5.5). Середній півперіод її коливань (Т ) буде приблизно дорівнювати пі-
р
вперіоду коливань прихованої періодичної складової.

1


0,75
1 2

0,5

i
t
i+1
0,25
t
i
0 t, c
0 1 2 3 4 5 6 7 8 9 10
 2
-0,25
 1 
i+1
-0,5

Рис. 5.5 – Нормовані кореляційні функції випадкових процесів за наявності
слабо (1) та сильно (2) вираженої періодичної складової коливань

Величину Т знаходять при цьому із виразу:
р
1 n
T р    t ( i 1  ) t ,
i
n i 0
де n – кількість півперіодів нормованої кореляційної функції;
t – послідовні значини абсцис точок перетину кореляційної функції 
і
з віссю t (див. рис. 5.5).
Виявлення півперіоду (а значить і періоду) коливань прихованої періодич-
ної складової дає можливість встановити генератор її формування. В кінцевому
рахунку це дозволяє розробити заходи щодо зменшення шкодочинності впливу
періодичних коливань на досліджуваний об’єкт, процес тощо.
Нормовані кореляційні функції з різними параметрами прихованої періоди-
чної складової можна порівняти між собою з допомогою декременту затухання .
Цей показник розраховують так:

1 m ρ
    ln i ,
m i 1 ρ i 1

де m – число пар суміжних екстремумів  і  нормованої кореляційної
і
і+1
функції (див. рис. 5.5).
Однією із найважливіших характеристик кореляційної функції є інтервал
кореляції. Зазвичай під ним розуміють час, на протязі якого кореляційних зв'язок
затухає або зникає взагалі.