Page 86 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

86

1

0,8

0,6

0,4
1
0,2

R 0

0 4 8 12 16 20 24 28 32 36 40
-0,2
2
-0,4

-0,6
L, м

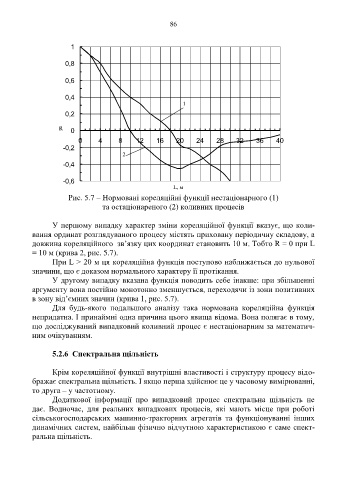
Рис. 5.7 – Нормовані кореляційні функції нестаціонарного (1)
та остаціонареного (2) коливних процесів

У першому випадку характер зміни кореляційної функції вказує, що коли-
вання ординат розглядуваного процесу містять приховану періодичну складову, а
довжина кореляційного зв’язку цих координат становить 10 м. Тобто R = 0 при L
= 10 м (крива 2, рис. 5.7).
При L > 20 м ця кореляційна функція поступово наближається до нульової
значини, що є доказом нормального характеру її протікання.
У другому випадку вказана функція поводить себе інакше: при збільшенні
аргументу вона постійно монотонно зменшується, переходячи із зони позитивних
в зону від’ємних значин (крива 1, рис. 5.7).
Для будь-якого подальшого аналізу така нормована кореляційна функція
непридатна. І принаймні одна причина цього явища відома. Вона полягає в тому,
що досліджуваний випадковий коливний процес є нестаціонарним за математич-
ним очікуванням.

5.2.6 Спектральна щільність

Крім кореляційної функції внутрішні властивості і структуру процесу відо-
бражає спектральна щільність. І якщо перша здійснює це у часовому вимірюванні,
то друга – у частотному.
Додаткової інформації про випадковий процес спектральна щільність не
дає. Водночас, для реальних випадкових процесів, які мають місце при роботі
сільськогосподарських машинно-тракторних агрегатів та функціонуванні інших
динамічних систем, найбільш фізично відчутною характеристикою є саме спект-
ральна щільність.