Page 85 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

85

Для випадкових процесів, зображених на рис. 5.5, за інтервал кореляції вва-
жать відрізок часу ( ,  ) від початку координат до першого перетину кореляцій-
1
2
ної функції з віссю абсцис.
Виходячи з цього, параметри  і  називають часом кореляційного зв’язку.
1
2
В дійсності вони, відображаючи час спадання кореляційної функції, характеризу-
ють частотний склад випадкових процесів. Більш низькочастотним із них є той, у
якого час кореляційного зв’язку більший. Саме таким є процес 1 у порівнянні з
процесом 2 (рис. 5.5), оскільки у першого час кореляційного зв’язку  = 2 с, а
1
другого –  = 1,2 с.
2
Інколи в практиці роботи сільськогосподарських агрегатів зустрічаються
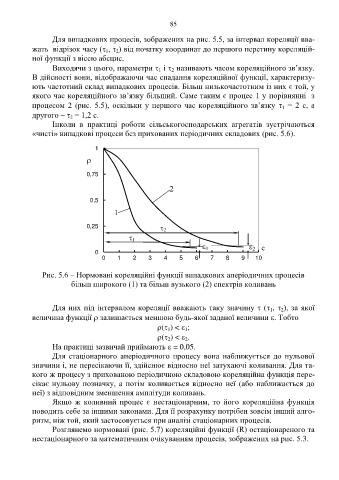
«чисті» випадкові процеси без прихованих періодичних складових (рис. 5.6).

1


0,75

2

0,5

1

0,25  2
 1
 1  2 с
0
0 1 2 3 4 5 6 7 8 9 10

Рис. 5.6 – Нормовані кореляційні функції випадкових аперіодичних процесів
більш широкого (1) та більш вузького (2) спектрів коливань

Для них під інтервалом кореляції вважають таку значину  ( ,  ), за якої
1
2
величина функції  залишається меншою будь-якої заданої величини . Тобто
( ) <  ;
1
1
( ) <  .
2
2
На практиці зазвичай приймають  = 0,05.
Для стаціонарного аперіодичного процесу вона наближується до нульової
значини і, не пересікаючи її, здійснює відносно неї затухаючі коливання. Для та-
кого ж процесу з прихованою періодичною складовою кореляційна функція пере-
сікає нульову позначку, а потім коливається відносно неї (або наближається до
неї) з відповідним зменшення амплітуди коливань.
Якщо ж коливний процес є нестаціонарним, то його кореляційна функція
поводить себе за іншими законами. Для її розрахунку потрібен зовсім інший алго-
ритм, ніж той, який застосовується при аналізі стаціонарних процесів.
Розглянемо нормовані (рис. 5.7) кореляційні функції (R) остаціонареного та
нестаціонарного за математичним очікуванням процесів, зображених на рис. 5.3.