Page 83 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

83

5.2.5 Кореляційна функція

Дуже часто таких статистичних характеристик, як середнє арифметичне (Х),
дисперсія (D) і коефіцієнт варіації (V) недостатньо для повної оцінки тієї чи іншої
випадкової функції. Два процеси з практично однаковими значинами Х, D і V мо-
жуть протікати абсолютно по різному.
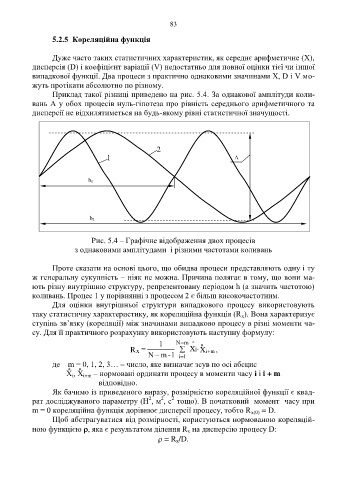
Приклад такої різниці приведено на рис. 5.4. За однакової амплітуди коли-
вань А у обох процесів нуль-гіпотеза про рівність середнього арифметичного та
дисперсії не відхилятиметься на будь-якому рівні статистичної значущості.

2
1 А

h 1

h 2

Рис. 5.4 – Графічне відображення двох процесів
з однаковими амплітудами і різними частотами коливань

Проте сказати на основі цього, що обидва процеси представляють одну і ту
ж генеральну сукупність – ніяк не можна. Причина полягає в тому, що вони ма-
ють різну внутрішню структуру, репрезентовану періодом h (а значить частотою)
коливань. Процес 1 у порівнянні з процесом 2 є більш високочастотним.
Для оцінки внутрішньої структури випадкового процесу використовують
таку статистичну характеристику, як кореляційна функція (R ). Вона характеризує
х
ступінь зв’язку (кореляції) між значинами випадково процесу в різні моменти ча-
су. Для її практичного розрахунку використовують наступну формулу:
1 N m 
Rx   Xi  Xi m ,
N  m 1 - i 1
де m = 0, 1, 2, 3… – число, яке визначає зсув по осі абсцис
Х , Х i+m – нормовані ординати процесу в моменти часу і і i + m
і
відповідно.
Як бачимо із приведеного виразу, розмірністю кореляційної функції є квад-
2
2
2
рат досліджуваного параметру (Н , м , с тощо). В початковий момент часу при
m = 0 кореляційна функція дорівнює дисперсії процесу, тобто R х(0) = D.
Щоб абстрагуватися від розмірності, користуються нормованою кореляцій-
ною функцією , яка є результатом ділення R на дисперсію процесу D:
х
 = R /D.
х