Page 94 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

94

Y

y =k-α∙e -βx
1

C

C
2
y =α∙x/(1-β∙x )
2
O X

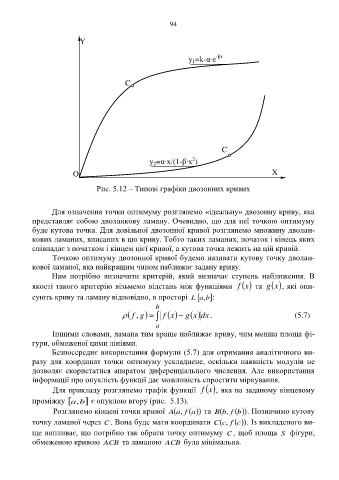
Рис. 5.12 – Типові графіки двозонних кривих

Для означення точки оптимуму розглянемо «ідеальну» двозонну криву, яка
представляє собою дволанкову ламану. Очевидно, що для неї точкою оптимуму

буде кутова точка. Для довільної двозонної кривої розглянемо множину дволан-
кових ламаних, вписаних в цю криву. Тобто таких ламаних, початок і кінець яких
співпадає з початком і кінцем цієї кривої, а кутова точка лежить на цій кривій.
Точкою оптимуму двозонної кривої будемо називати кутову точку дволан-
кової ламаної, яка найкращим чином наближає задану криву.
Нам потрібно визначити критерій, який визначає ступень наближення. В
якості такого критерію візьмемо відстань між функціями   xf та   xg , які опи-
сують криву та ламану відповідно, в просторі  baL , :
b
 f , g    f   gx  dxx . (5.7)
a
Іншими словами, ламана тим краще наближає криву, чим менша площа фі-
гури, обмеженої цими лініями.
Безпосереднє використання формули (5.7) для отримання аналітичного ви-
разу для координат точки оптимуму ускладнене, оскільки наявність модулів не
дозволяє скористатися апаратом диференціального числення. Але використання
інформації про опуклість функції дає можливість спростити міркування.
Для прикладу розглянемо графік функції   xf , яка на заданому кінцевому

проміжку a, b  є опуклою вгору (рис. 5.13).
Розглянемо кінцеві точки кривої aA , f   та bB , f  . Позначимо кутову
b
a
c
точку ламаної через C . Вона буде мати координати cC , f  . Із викладеного ви-
ще випливає, що потрібно так обрати точку оптимуму C , щоб площа S фігури,
обмеженою кривою ACB та ламаною ACB була мінімальна.