Page 96 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

96

Цілком зрозуміло, що вираз (5.10) можна використовувати для аналітичного
визначення положення (координат) точки C . В якості прикладу розглянемо функцію

x
y  . (5.11)

1  2
x
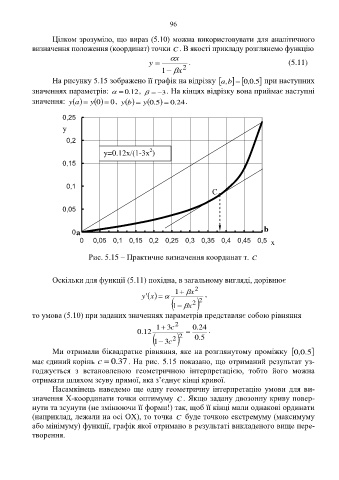
На рисунку 5.15 зображено її графік на відрізку  ,ba   0,0  5 . при наступних
значеннях параметрів:   . 0 12,    3. На кінцях відрізку вона приймає наступні
значення:    yay   00  ,    yby  5.0   . 0 24.

0,25
y

0,2
2
y=0.12х/(1-3х )
0,15

0,1
С

0,05

0 a b
0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 x

Рис. 5.15 – Практичне визначення координат т. C

Оскільки для функції (5.11) похідна, в загальному вигляді, дорівнює

1  x 2

y   x   ,
 1  x 2  2
то умова (5.10) при заданих значеннях параметрів представляє собою рівняння

1 3c 2 . 0 24
. 0 12 2  .
 1 3c 2  5 . 0
Ми отримали біквадратне рівняння, яке на розглянутому проміжку  0,0 5 . 
має єдиний корінь c . 0 37 . На рис. 5.15 показано, що отриманий результат уз-
годжується з встановленою геометричною інтерпретацією, тобто його можна
отримати шляхом зсуву прямої, яка з’єднує кінці кривої.
Насамкінець наведемо ще одну геометричну інтерпретацію умови для ви-
значення Х-координати точки оптимуму C . Якщо задану двозонну криву повер-
нути та зсунути (не змінюючи її форми!) так, щоб її кінці мали однакові ординати
(наприклад, лежали на осі ОХ), то точка C буде точкою екстремуму (максимуму
або мінімуму) функції, графік якої отримано в результаті викладеного вище пере-
творення.