Page 95 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

95

Зрозуміло, що для фіксованої кривої величина S буде залежати тільки від
положення точки C , тобто S  S   c . В силу опуклості кривої ACB матимемо, що
ламана лежить під кривою, а, отже S дорівнює різниці площ, обмежених кривою
та ламаною.
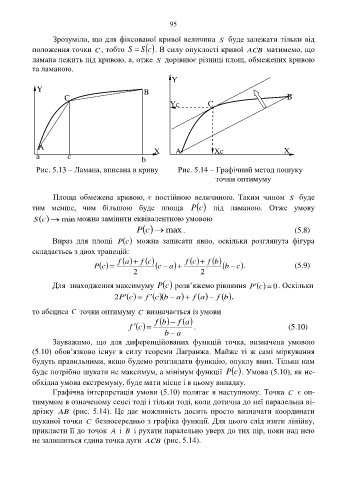
Y
Y B
C B
Yc C

A X A Xc X
a c b

Рис. 5.13 – Ламана, вписана в криву Рис. 5.14 – Графічний метод пошуку
точки оптимуму

Площа обмежена кривою, є постійною величиною. Таким чином S буде
тим менше, чим більшою буде площа P   c під ламаною. Отже умову

S   c min можна замінити еквівалентною умовою

 cP max . (5.8)
Вираз для площі   cP можна записати явно, оскільки розглянута фігура
складаєтьсь з двох трапецій:
f   a  f   c f   c  f   b
P   c  c   a  b   c . (5.9)
2 2

Для знаходження максимуму   cP розв’яжемо рівняння   cP  0. Оскільки
c
2 P    f   bc  a  f   f  ,
b
a
то абсциса c точки оптимуму C визначається із умови
f   b  f   a
  cf   . (5.10)
b  a
Зауважимо, що для диференційованих функцій точка, визначена умовою
(5.10) обов’язково існує в силу теореми Лагранжа. Майже ті ж самі міркування
будуть правильними, якщо будемо розглядати функцію, опуклу вниз. Тільки нам
буде потрібно шукати не максимум, а мінімум функції   cP . Умова (5.10), як не-

обхідна умова екстремуму, буде мати місце і в цьому випадку.
Графічна інтерпретація умови (5.10) полягає в наступному. Точка C є оп-
тимумом в означеному сенсі тоді і тільки тоді, коли дотична до неї паралельна ві-
дрізку AB (рис. 5.14). Це дає можливість досить просто визначати координати
шуканої точки C безпосередньо з графіка функції. Для цього слід взяти лінійку,
прикласти її до точок A і B і рухати паралельно уверх до тих пір, поки над нею

не залишиться єдина точка дуги ACB (рис. 5.14).