Page 40 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

40

Розглянемо наступний простий приклад. Нехай у процесі робочого руху на
динамічну систему  причіпну валкову жниварку  діють наступні сили (рис. 3.5):
- сила опору (R) стеблового масиву;
- сили опору коченню лівого (P ) та правого (P ) опорних коліс жниварки;
f1
f2
- бокові сили лівого (Т ) та правого (Т ) опорних коліс жниварки.
1
2
Під сумарним впливом цих сил причіпна машина відхиляється від прямолі-
нійного руху на кут .

О
a
l b P f1


c P f2

R
T 1
d
T 2

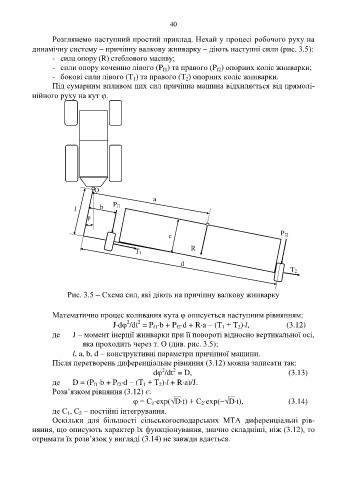
Рис. 3.5  Схема сил, які діють на причіпну валкову жниварку

Математично процес коливання кута  описується наступним рівнянням:
2
2
Jd /dt = P b + P d + Ra  (Т + Т )l, (3.12)
f1
f2
1
2
де J  момент інерції жниварки при її повороті відносно вертикальної осі,
яка проходить через т. О (див. рис. 3.5);
l, a, b, d  конструктивні параметри причіпної машини.
Після перетворень диференціальне рівняння (3.12) можна записати так:
2
2
d /dt = D, (3.13)
де D = (P b + P d  (Т + Т )l + Ra)/J.
f2
f1
1
2
Розв’язком рівняння (3.12) є:
 = С exp(√Dt) + С exp(√Dt), (3.14)
1
2
де С , С  постійні інтегрування.
2
1
Оскільки для більшості сільськогосподарських МТА диференціальні рів-
няння, що описують характер їх функціонування, значно складніші, ніж (3.12), то
отримати їх розв’язок у вигляді (3.14) не завжди вдається.