Page 75 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

75

Більшість коливних явищ у сільськогосподарському виробництві представ-
ляють собою випадкові стаціонарні і ергодичні процеси. Механізми їх обробітку
нині практично повністю формалізовані і при використанні комп’ютерів з відпо-
відним програмним забезпеченням не викликають будь-яких труднощів.
Нестаціонарність того чи іншого випадкового процесу може бути за мате-
матичним очікуванням, дисперсією і за тим та другим одночасно.
Коли має місце нестаціонарність за дисперсією, то, за рекомендацією проф.
А.Б. Лур’є, нестаціонарну ділянку слід просто видалити (рис. 5.1), а решту даних
обробляти як єдину генеральну сукупність.

6
5
4
3
2
1
0
14
12
0 2 4 6 8 10 нестаціонарність за 18 20 22 24 26
16
дисперсією

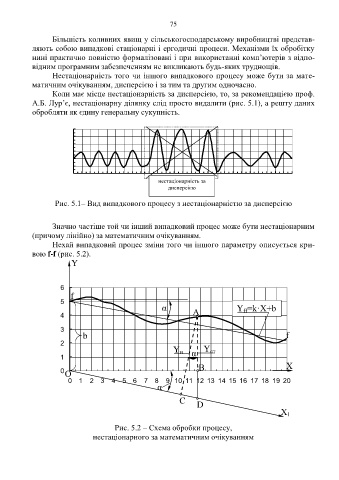
Рис. 5.1– Вид випадкового процесу з нестаціонарністю за дисперсією

Значно частіше той чи інший випадковий процес може бути нестаціонарним
(причому лінійно) за математичним очікуванням.
Нехай випадковий процес зміни того чи іншого параметру описується кри-
вою f-f (рис. 5.2).
Y

6
f
5
α Y =k·X+b
ff
4 А

3
b f
2
Y α Y
ст
н
1
В Х
0 О
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
α

С D
Х
1
Рис. 5.2 – Схема обробки процесу,
нестаціонарного за математичним очікуванням