Page 30 - МНД_ПЗ

Таким чином, рішення диференційного рівняння (2) має вид:

 = ocost

 2Rx L 

Або    cos  t (5)
o  m  2 
 R 
Моделювання коливань котка у поздовжньо-вертикальній

площині.

В діапазон комірок В1:В5 електронної таблиці Excel послідовно

заносимо значини Rx, L, m, R і о. Величину останньої задаємо в ме-

0
жах 1...3 .

Rx = 2000
L = 2
m = 300
R = 0,25
 = 1 0,017444
о
k = 20,65591
t = 0 1 2 3 4 5
 = 1 -0,233 -0,891 0,649 0,588 -0,924
i

В комірці В6 за формулою =КОРЕНЬ(2*В1*В2/(В3*В4^2) розмі-
 = 0,017 -0,004 -0,016 0,011 0,010 -0,016
i
щуємо значину підкорінного виразу формули (5).

В комірки сьомої строчки електронної таблиці вводимо значини

часу (від нуля до 10 с, наприклад).

В комірці В8 розміщуємо результат розрахунку значини кута 

за формулою =$B$5*COS($B$6*B$7). Вказану формулу копіюємо у

відповідні комірки восьмої строчки електронної таблиці.

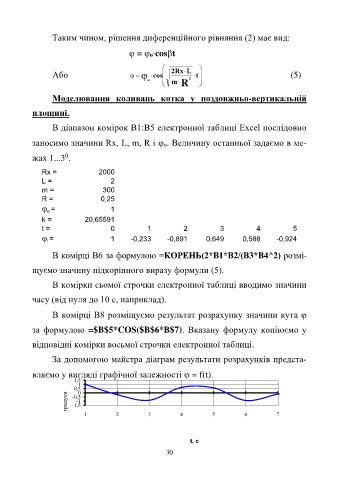
За допомогою майстра діаграм результати розрахунків предста-

вляємо у вигляді графічної залежності  = f(t).
1,5
1
0,5
0
градуси -0,5
-1
-1,5
1 2 3 4 5 6 7

t, c
30