Page 54 - МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

54

600

500 0

400
A B
X 2 300
Ф
200 max
Ф 1
100 C

0 D 500
0
0 100 200 300 400 500 600 700 800 900 1000

X 1

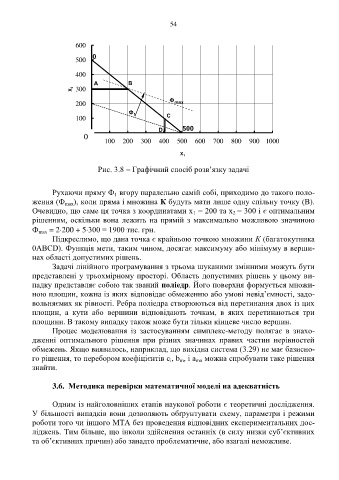
Рис. 3.8  Графічний спосіб розв’язку задачі

Рухаючи пряму Ф вгору паралельно самій собі, приходимо до такого поло-
1
ження (Ф max ), коли пряма і множина К будуть мати лише одну спільну точку (В).
Очевидно, що саме ця точка з координатами х = 200 та х = 300 і є оптимальним
2
1
рішенням, оскільки вона лежить на прямій з максимально можливою значиною
Ф max = 2200 + 5300 = 1900 тис. грн.
Підкреслимо, що дана точка є крайньою точкою множини К (багатокутника
0ABCD). Функція мети, таким чином, досягає максимуму або мінімуму в верши-
нах області допустимих рішень.

Задачі лінійного програмування з трьома шуканими змінними можуть бути
представлені у трьохмірному просторі. Область допустимих рішень у цьому ви-
падку представляє собою так званий поліедр. Його поверхня формується множи-
ною площин, кожна із яких відповідає обмеженню або умові невід’ємності, задо-
вольняємих як рівності. Ребра поліедра створюються від перетинання двох із цих
площин, а кути або вершини відповідають точкам, в яких перетинаються три
площини. В такому випадку також може бути тільки кінцеве число вершин.
Процес моделювання із застосуванням симплекс-методу полягає в знахо-
дженні оптимального рішення при різних значинах правих частин нерівностей
обмежень. Якщо виявилось, наприклад, що вихідна система (3.29) не має базисно-
го рішення, то перебором коефіцієнтів с , b , і a можна спробувати таке рішення
mn
m
і
знайти.

3.6. Методика перевірки математичної моделі на адекватність

Одним із найголовніших етапів наукової роботи є теоретичні дослідження.
У більшості випадків вони дозволяють обґрунтувати схему, параметри і режими
роботи того чи іншого МТА без проведення відповідних експериментальних дос-
ліджень. Тим більше, що інколи здійснення останніх (в силу низки суб’єктивних
та об’єктивних причин) або занадто проблематичне, або взагалі неможливе.